Research

Table of non-hyperelliptic new modular Jacobians 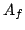of dimension 3

curves	Dixmier-invariants
$X_{97}^{A}$	$i_1=\frac{-23^9}{2^{53}\cdot3^{27}\cdot97^{3}}$
	$i_2=\frac{5^2 \cdot 23^7}{2^{57}\cdot 3^{29} \cdot 97^{3}}$
	$i_3=\frac{23^6 \cdot 109 }{2^{39}\cdot 3^{24}\cdot 97^3}$
	$i_4=\frac{-23^5 \cdot 106649}{2^{37}\cdot 3^{25}\cdot 97^3}$
	$i_5=\frac{7 \cdot 13 \cdot 23^4 \cdot 29 \cdot 47}{2^{32}\cdot 3^{23}\cdot 97^3}$
	$i_6=\frac{7 \cdot 23^3 \cdot 4446899}{2^{29}\cdot 3^{22} \cdot 97^3}$
$X_{109}^{B}$	$i_1=\frac{11^9}{2^{53}\cdot 3^{27}\cdot 109^3}$
	$i_2=\frac{11^7\cdot 47^2}{2^{57} \cdot 3^{29} \cdot 109^3}$
	$i_3=\frac{11^6\cdot 101\cdot 1259}{2^{43}\cdot 3^{24}\cdot 109^3}$
	$i_4=\frac{11^5\cdot 5894347}{ 2^{40} \cdot 3^{25} \cdot 109^3}$
	$i_5=\frac{11^5\cdot 5087\cdot 10889}{2^{37}\cdot 3^{23} \cdot 109^3}$
	$i_6=\frac{5\cdot 11^3 \cdot 39330808093}{2^{36} \cdot 3^{22} \cdot 109^3}$
$X_{113}^{C}$	$i_1=\frac{-1}{2^{53} \cdot 3^{27}\cdot 113^3}$
	$i_2=\frac{13 \cdot 61}{2^{57} \cdot 3^{29} \cdot 113^3}$
	$i_3=\frac{-19\cdot 23\cdot 269}{2^{43} \cdot 3^{24} \cdot 113^3}$
	$i_4=\frac{-836063}{2^{39} \cdot 3^{25} \cdot 113^3}$
	$i_5=\frac{5\cdot 13\cdot 38562143}{2^{37} \cdot 3^{23} 113^3}$
	$i_6=\frac{-11\cdot 37\cdot 62711911}{2^{36} \cdot 3^{22} \cdot 113^3}$
$X_{127}^{A}$	$i_1=\frac{71^9}{2^{53} \cdot 3^{27} \cdot 127^3}$
	$i_2=\frac{-43\cdot 71^{7} \cdot 139}{ 2^{57} \cdot 3^{29}\cdot 127^3}$
	$i_3=\frac{7 \cdot 71^6 \cdot 13933}{2^{40} \cdot 3^{24} 127^{3}}$
	$i_4=\frac{-7 \cdot 71^5 \cdot 23840251}{2^{41} \cdot 3^{25} \cdot 127^3}$
	$i_5=\frac{13\cdot 71^4 \cdot 1336920521}{2^{38} 3^{23}\cdot 127^3}$
	$i_6=\frac{53\cdot 71^3 \cdot 607\cdot 3251\cdot 26681}{2^{36} \cdot 3^{22} \cdot 127^3}$
$X_{139}^{B}$	$i_1=\frac{-17^9}{2^{53} \cdot 3^{27} \cdot 139^3 }$
	$i_2=\frac{13\cdot17^7\cdot349}{2^{57}\cdot 3^{29} 139^3}$
	$i_3=\frac{-7 \cdot17^6\cdot41 \cdot367}{2^{43}\cdot 3^{24} \cdot 139^3}$
	$i_4=\frac{-7 \cdot17^5 \cdot 2835667}{2^{40} \cdot 3^{25} \cdot 139^3}$
	$i_5=\frac{5 \cdot7 \cdot 17^5\cdot 383 \cdot 12161}{2^{34} \cdot 3^{23} \cdot 139^3}$
	$i_6=\frac{7 \cdot 11 \cdot17^3\cdot 53 \cdot 149854519}{2^{36} \cdot 3^{22} \cdot 139^3}$

curves	Dixmier-invariants
$X_{149}^{A}$	$i_1=\frac{83^9}{2^{53}\cdot 3^{27} \cdot 149^3}$
	$i_2=\frac{83^7\cdot 1823}{2^{57}\cdot 3^{29}\cdot 149^3}$
	$i_3=\frac{5 \cdot 83^6\cdot 239 \cdot 947}{2^{41} \cdot 3^{24} \cdot 149^3}$
	$i_4=\frac{83^5\cdot 432110321}{2^{41} \cdot 3^{25} \cdot 149^3}$
	$i_5=\frac{7 \cdot83^4\cdot 236140337759}{2^{38}\cdot 3^{23} \cdot 149^3}$
	$i_6=\frac{5 \cdot7 \cdot17 \cdot23 \cdot83^3\cdot 239 \cdot853 \cdot 58049}{2^{36}\cdot 3^{22} \cdot149^3}$
$X_{151}^{A}$	$i_1=\frac{7^9}{ 2^{53} \cdot 3^{27} \cdot 151^3}$
	$i_2=\frac{-7^7 \cdot 17 \cdot 617 }{ 2^{57} \cdot 3^{29} \cdot 151^3}$
	$i_3=\frac{7^6 \cdot 23 \cdot 251 \cdot 577 }{ 2^{43} \cdot 3^{24} \cdot 151^3}$
	$i_4=\frac{7^5 \cdot 11\cdot 1621 \cdot 5087 }{ 2^{40} \cdot 3^{25} \cdot 151^{3}}$
	$i_5=\frac{-7^4 \cdot 31 \cdot 37 \cdot 113 \cdot 587 \cdot 6733 }{ 2^{37} \cdot 3^{23} \cdot 151^3}$
	$i_6=\frac{7^3 \cdot 38767 \cdot 945648167 }{ 2^{36} \cdot 3^{22} \cdot 151^3}$
$X_{169}^{B}$	$i_1=\frac{5^{18} }{ 2^{53} \cdot 3^{27} \cdot 13^{6}}$
	$i_2=\frac{-5^{14} \cdot 7\cdot 79}{ 2^{57} \cdot 3^{29} \cdot 13^{6}}$
	$i_3=\frac{5^{12} \cdot 155887 }{2^{43} \cdot 3^{24} \cdot 13^6}$
	$i_4=\frac{5^{10} \cdot 11 \cdot 216829 }{ 2^{39} \cdot 3^{25} \cdot 13^{6} }$
	$i_5=\frac{5^8 \cdot 131 \cdot 463 \cdot 69847 }{ 2^{37} \cdot 3^{23} \cdot 13^6}$
	$i_6=\frac{5^8 \cdot 89\cdot 162518641}{ 2^{36} \cdot 3^{22} \cdot 13^6}$
$X_{179}^{B}$	$i_1=\frac{-17^9 }{ 2^{53} \cdot 3^{27} \cdot 179^3}$
	$i_2=\frac{17^8 \cdot 89}{2^{57} \cdot 3^{29} \cdot 179^3}$
	$i_3=\frac{5^3 \cdot 13 \cdot 17^7 }{ 2^{41} \cdot 3^{24} \cdot 179^{3}}$
	$i_4=\frac{-7 \cdot 17^6 \cdot 89 \cdot 227 }{ 2^{41} \cdot 3^{25} \cdot 179^{3} }$
	$i_5=\frac{17^5 \cdot 41 \cdot 2478937 }{2^{38} \cdot 3^{23} \cdot 179^3}$
	$i_6=\frac{-17^3 \cdot 36829407137}{ 2^{36} \cdot 3^{22} \cdot 179^3}$
$X_{187}^{E}$	$i_1=\frac{7^9}{ 2^{44} \cdot 3^{27} \cdot 11^{3} \cdot 17^4}$
	$i_2=\frac{-7^7 \cdot 59}{ 2^{48} \cdot 3^{29} \cdot 11^3 \cdot 17^3}$
	$i_3=\frac{5 \cdot 7^6 \cdot 157 \cdot 283}{ 2^{35} \cdot 3^{24} \cdot 11^{3} \cdot 17^4}$
	$i_4=\frac{-7^5 \cdot 13 \cdot 16456963 }{ 2^{36} \cdot 3^{25} \cdot 11^{3} \cdot 17^4}$
	$i_5=\frac{7^4 \cdot 111770067821 }{2^{34} \cdot 3^{23} \cdot 11^{3} \cdot 17^4}$
	$i_6=\frac{-7^3 \cdot 37 \cdot 131 \cdot 181 \cdot 101419 }{ 2^{32} \cdot 3^{22} \cdot 11^3 \cdot 17^4}$

curves	Dixmier-invariants
$X_{203}^{F}$	$i_1=\frac{7^4 \cdot 17^9 }{ 2^{53} \cdot 3^{27} \cdot 29^3}$
	$i_2=\frac{5^3 \cdot 7^2 \cdot 17^7 \cdot 283 }{ 2^{57} \cdot 3^{29} \cdot 29^{3}}$
	$i_3=\frac{5 \cdot 7 \cdot 17^6 \cdot 353 \cdot 29327 }{ 2^{43} \cdot 3^{24} \cdot 29^3}$
	$i_4=\frac{7^2 \cdot 17^5 \cdot 487 \cdot 216577 }{2^{40} \cdot 3^{25} \cdot 29^3}$
	$i_5=\frac{17^4 \cdot 6737 \cdot 8849 \cdot 359417 }{2^{36} \cdot 3^{23} \cdot 7 \cdot 29^3}$
	$i_6=\frac{17^3 \cdot 149 \cdot 131679238350523 }{2^{36} \cdot 3^{22} \cdot 7^2\cdot 29^3}$
$X_{217}^{A}$	$i_1=\frac{5^9 \cdot 227^9}{2^{53} \cdot 3^{55} \cdot 7^3 \cdot 31^3}$
	$i_2=\frac{-5^8 \cdot 227^7 \cdot 342821}{2^{57} \cdot 3^{57} \cdot 7^3 \cdot 31^3}$
	$i_3=\frac{5^6 \cdot 227^6 \cdot 439 \cdot 3871663 }{2^{39} \cdot 3^{52} \cdot 7^3 \cdot 31^3}$
	$i_4=\frac{5^5 \cdot 19 \cdot 113 \cdot 227^5 \cdot 3181 \cdot 4410097 }{2^{41} \cdot 3^{53} \cdot 7^3 \cdot 31^3 }$
	$i_5=\frac{5^4 \cdot 227^4 \cdot 3264116968231423459}{2^{38} \cdot 3^{51} \cdot 7^3\cdot 31^3}$
	$i_6=\frac{5^3 \cdot 227^3 \cdot 11320571 \cdot 514794731537767 }{2^{36} \cdot 3^{50} \cdot 7^3 \cdot 31^3}$
$X_{239}^{A}$	$i_1=\frac{5^9 \cdot 7^9}{2^{53} \cdot 3^{27} \cdot 239^3}$
	$i_2=\frac{-5^7 \cdot 7^7 \cdot 433}{2^{57} \cdot 3^{29} \cdot 239^3}$
	$i_3=\frac{-5^6 \cdot 7^6 \cdot 43963}{2^{39} \cdot 3^{24} \cdot 239^3}$
	$i_4=\frac{-5^5 \cdot 7^5 \cdot 509 \cdot 112481 }{2^{41} \cdot 3^{25} \cdot 239^3 }$
	$i_5=\frac{-5^4 \cdot 7^4 \cdot 27827 \cdot 3496799}{2^{38} \cdot 3^{23} \cdot 239^3}$
	$i_6=\frac{-5^4 \cdot 7^3 \cdot 68503144613}{2^{36} \cdot 3^{22} \cdot 239^3}$
$X_{295}^{A}$	$i_1=\frac{-11^9}{2^{53} \cdot 3^{27} \cdot 5^3 \cdot 59^3}$
	$i_2=\frac{11^7 \cdot 13 \cdot 181}{2^{57} \cdot 3^{29} \cdot 5^3 \cdot 59^3}$
	$i_3=\frac{-7 \cdot 11^6 \cdot 23203}{2^{42} \cdot 3^{24} \cdot 5^3 \cdot 59^3}$
	$i_4=\frac{-7^2 \cdot 11^5 \cdot 370631}{2^{41} \cdot 3^{25} \cdot 5^3 \cdot 59^3}$
	$i_5=\frac{7 \cdot 11^5 \cdot 19\cdot 769 \cdot 2287}{2^{38} \cdot 3^{23} \cdot 5^2 \cdot 59^3}$
	$i_6=\frac{-7 \cdot 11^3 \cdot 197 \cdot 415664659 }{2^{36} \cdot 3^{22} \cdot 5^3 \cdot 59^3}$
$X_{329}^{C}$	$i_1=\frac{-19^9}{2^{53} \cdot 3^{27} \cdot 7^3 \cdot 47^3}$
	$i_2=\frac{5 \cdot 19^7 \cdot 1181}{2^{57} \cdot 3^{29} \cdot 7^3 \cdot 47^3}$
	$i_3=\frac{-19^6 \cdot 29 \cdot 61 \cdot 67}{2^{40} \cdot 3^{24} \cdot 7^3 \cdot 47^3}$
	$i_4=\frac{-13 \cdot 19^5 \cdot 701\cdot 7723 }{2^{41} \cdot 3^{25} \cdot 7^3 \cdot 47^3}$
	$i_5=\frac{19^4 \cdot 163061001821 }{2^{38} \cdot 3^{23} \cdot 7^3 \cdot 47^3}$
	$i_6=\frac{5 \cdot 19^3 \cdot 41 \cdot 7369 \cdot 904573 }{2^{36} \cdot 3^{22} \cdot 7^3 \cdot 47^3}$

curves	Dixmier-invariants
$X_{369}^{D}$	$i_1=\frac{7^9}{2^{44} \cdot 3^{18} \cdot 41^3}$
	$i_2=\frac{-7^7 \cdot 97 }{2^{48} \cdot 3^{21} \cdot 41^3}$
	$i_3=\frac{7^6 \cdot 6353 }{2^{36} \cdot 3^{16} \cdot 41^3}$
	$i_4=\frac{7^5 \cdot 73 \cdot 31337}{2^{36} \cdot 3^{18} \cdot 41^3}$
	$i_5=\frac{7^4 \cdot 43 \cdot 4662331 }{2^{34} \cdot 3^{15} \cdot 41^3}$
	$i_6=\frac{-7^3 \cdot 1307 \cdot 1601 \cdot 5303 }{2^{32} \cdot 3^{16} \cdot 41^3}$
$X_{369}^{E}$	$i_1=\frac{7^9}{2^{44} \cdot 3^{18} \cdot 41^3}$
	$i_2=\frac{-7^7 \cdot 97 }{2^{48} \cdot 3^{21} \cdot 41^3}$
	$i_3=\frac{7^6 \cdot 6353 }{2^{36} \cdot 3^{16} \cdot 41^3}$
	$i_4=\frac{7^5 \cdot 73 \cdot 31337}{2^{36} \cdot 3^{18} \cdot 41^3}$
	$i_5=\frac{7^4 \cdot 43 \cdot 4662331 }{2^{34} \cdot 3^{15} \cdot 41^3}$
	$i_6=\frac{-7^3 \cdot 1307 \cdot 1601 \cdot 5303 }{2^{32} \cdot 3^{16} \cdot 41^3}$
$X_{388}^{A}$	$i_1=\frac{-1}{ 2^{46} \cdot 3^{27} \cdot 97^3}$
	$i_2=\frac{-233}{2^{50} \cdot 3^{29} \cdot 97^3}$
	$i_3=\frac{5293513}{2^{41} \cdot 3^{24} \cdot 97^3}$
	$i_4=\frac{624203}{2^{35} \cdot 3^{25} \cdot 97^3}$
	$i_5=\frac{71 \cdot 3533 \cdot 300997}{2^{38} \cdot 3^{23} \cdot 97^3}$
	$i_6=\frac{-29 \cdot 409326261863}{2^{36} \cdot 3^{22} \cdot 97^3}$
$X_{436}^{B}$	$i_1=\frac{181^9}{2^{37} \cdot 3^{18} \cdot 11^{14} \cdot 109^3}$
	$i_2=\frac{-5\cdot 23\cdot 113\cdot 181^7}{2^{42} \cdot 3^{20} \cdot 11^{14} \cdot 109^3}$
	$i_3=\frac{181^6 \cdot 4727066557}{2^{35} \cdot 3^{15} \cdot 11^{14} \cdot 109^3}$
	$i_4=\frac{181^5 \cdot 499\cdot 56343733}{2^{33} \cdot 3^{15} \cdot 11^{14} \cdot 109^3}$
	$i_5=\frac{151\cdot 181^4 \cdot 381481\cdot 538018951}{2^{34} \cdot 3^{14} \cdot 11^{14} \cdot 109^3}$
	$i_6=\frac{181^3 \cdot 239273\cdot 480133\cdot 133676033}{2^{32} \cdot 3^{14} \cdot 11^{14} \cdot 109^3}$
$X_{452}^{A}$	$i_1=\frac{31^9}{2^{10} \cdot 3^{41} \cdot 113^3}$
	$i_2=\frac{13\cdot 17\cdot 31^7 \cdot 521}{2^{21} \cdot 3^{43} \cdot 113^3}$
	$i_3=\frac{31^6 \cdot 157\cdot 336931631}{2^{17} \cdot 3^{38} \cdot 113^3}$
	$i_4=\frac{5\cdot 31^5 \cdot 71\cdot 53551058051}{2^{18} \cdot 3^{39} \cdot 113^3}$
	$i_5=\frac{5\cdot 31^4 \cdot 774401181277897891}{2^{22} \cdot 3^{37} \cdot 113^3}$
	$i_6=\frac{7\cdot 23\cdot 31^3 \cdot 421\cdot 10301727084532427}{2^{22} \cdot 3^{36} \cdot 113^3}$

curves	Dixmier-invariants
$X_{475}^{E}$	$i_1=\frac{3067^9}{2^{53} \cdot 3^{27} \cdot 5^6 \cdot 19^3}$
	$i_2=\frac{479\cdot 3067^7 \cdot 15937}{2^{57} \cdot 3^{29} \cdot 5^6 \cdot 19^3}$
	$i_3=\frac{193\cdot 3067^6 \cdot 115419877}{2^{39} \cdot 3^{24} \cdot 5^6 \cdot 19^3}$
	$i_4=\frac{41\cdot 3067^5 \cdot 41903\cdot 2234129}{2^{37} \cdot 3^{25} \cdot 5^4 \cdot 19^3}$
	$i_5=\frac{13\cdot 397\cdot 479\cdot 3067^4 \cdot 6619\cdot 8887\cdot 25349}{2^{32} \cdot 3^{23} \cdot 5^6 \cdot 19^3}$
	$i_6=\frac{3067^3 \cdot 1587899065951933060901}{2^{29} \cdot 3^{22} \cdot 5^5 \cdot 19^3}$
$X_{475}^{G}$	$i_1=\frac{3067^9}{2^{53} \cdot 3^{27} \cdot 5^6 \cdot 19^3}$
	$i_2=\frac{479\cdot 3067^7 \cdot 15937}{2^{57} \cdot 3^{29} \cdot 5^6 \cdot 19^3}$
	$i_3=\frac{193\cdot 3067^6 \cdot 115419877}{2^{39} \cdot 3^{24} \cdot 5^6 \cdot 19^3}$
	$i_4=\frac{41\cdot 3067^5 \cdot 41903\cdot 2234129}{2^{37} \cdot 3^{25} \cdot 5^4 \cdot 19^3}$
	$i_5=\frac{13\cdot 397\cdot 479\cdot 3067^4 \cdot 6619\cdot 8887\cdot 25349}{2^{32} \cdot 3^{23} \cdot 5^6 \cdot 19^3}$
	$i_6=\frac{3067^3 \cdot 1587899065951933060901}{2^{29} \cdot 3^{22} \cdot 5^5 \cdot 19^3}$
$X_{511}^{B}$	$i_1=\frac{5^9 \cdot 37^9 \cdot 43133^9}{2^{53} \cdot 3^{30} \cdot 7^8 \cdot 11^{14} \cdot 73^3 \cdot 101^{14}}$
	$i_2=\frac{-5^8 \cdot 37^7 \cdot 263\cdot 43133^7 \cdot 197689\cdot 6021091}{2^{57} \cdot 3^{32} \cdot 7^8 \cdot 11^{14} \cdot 73^3 \cdot 101^{14}}$
	$i_3=\frac{5^6 \cdot 13\cdot 37^6 \cdot 43133^6 \cdot 142702121\cdot 25535098000501}{2^{43} \cdot 3^{28} \cdot 7^8 \cdot 11^{14} \cdot 73^3 \cdot 101^{14}}$
	$i_4=\frac{5^5 \cdot 17\cdot 37^5 \cdot 577\cdot 43133^5 \cdot 3563719\cdot 164... ...791737}{2^{39} \cdot 3^{28} \cdot 7^8 \cdot 11^{14} \cdot 73^3 \cdot 101^{14}}$
	$i_5=\frac{-5^4 \cdot 13^2 \cdot 37^4 \cdot 43133^4 \cdot 411537604667032828532... ...0589099}{2^{33} \cdot 3^{24} \cdot 7^8 \cdot 11^{14} \cdot 73^3 \cdot 101^{14}}$
	$i_6=\frac{-5^3 \cdot 37^3 \cdot 43133^3 \cdot 688333\cdot 28685999 \cdot 30314... ...642759}{2^{36} \cdot 3^{26} \cdot 7^8 \cdot 11^{14} \cdot 73^3 \cdot 101^{14}}$
$X_{567}^{H}$	$i_1=\frac{5^4}{2^{53} \cdot 3^9 \cdot 7^3}$
	$i_2=\frac{5 \cdot 17}{2^{57} \cdot 3^{12} \cdot 7^3}$
	$i_3=\frac{5 \cdot 3821}{2^{42} \cdot 3^8 \cdot 7^3}$
	$i_4=\frac{17 \cdot 8363}{2^{41} \cdot 3^9 \cdot 5 \cdot 7^3}$
	$i_5=\frac{5^2 \cdot 313}{2^{38} \cdot 3^6 \cdot 7^3}$
	$i_6=\frac{-19 \cdot 83 \cdot 11119}{2^{36} \cdot 3^7 \cdot 5^2 \cdot 7^3}$
$X_{596}^{A}$	$i_1=\frac{359^9}{2^{55} \cdot 3^{27} \cdot 149^3}$
	$i_2=\frac{13 \cdot 23 \cdot 73 \cdot 359^7}{2^{57} \cdot 3^{29} \cdot 149^3}$
	$i_3=\frac{23 \cdot 359^6 \cdot 89348191}{2^{47} \cdot 3^{24} \cdot 149^3}$
	$i_4=\frac{5^2 \cdot 359^5 \cdot 39644905697}{2^{45} \cdot 3^{25} \cdot 149^3}$
	$i_5=\frac{47 \cdot 359^4 \cdot 370708577229919}{2^{42} \cdot 3^{23} \cdot 149^3}$
	$i_6=\frac{13 \cdot 19 \cdot 359^3 \cdot 16529 \cdot 794641 \cdot 2599117}{2^{40} \cdot 3^{22} \cdot 149^3}$

This table appears in :

R. Oyono: Non-hyperelliptic modular Jacobians of dimension 3, Mathematics of Computation, 78 (2009), no. 266, 1173-1191.

Last update November 17, 2011